本周三上课讲到了投资组合收益率的计算,课本上的例题把收益率计算涉及到的数据都给全了,同学们做了一个带概率的加权平均收益率计算。从课堂反应来看,似乎同学们都能明白例题的计算过程;从课堂提问情况来看,似乎同学们又没明白计算过程背后的数据信息。我在课后便针对收益率问题,做了一个梳理,查阅了好几个教材,发现该主题的例题几乎如出一辙,不同的仅为参数的调整。
为了换个思路来学习这个知识点,算是自我再学习,也是算我给学生们的答疑解惑。因刚好处在一周的因疫情居家隔离期间,消磨时间,我设计了一个案例:从中国股市中任意选取4支股票(实际上,我编写的python程序可以处理N多支股票的组合),用1年的日交易收盘价(可以是N年的数据)来计算确定股票投资组合的收益率及风险。
介绍该案例的目的是让我的学生们懂得实务中的收益率是怎么计算出来的,风险是怎么度量的,数据是如何取得的,数据是如何处理的......,最终,这么大、这么复杂的数据是怎么通过python程序计算的......
本文先介绍收益率,下一篇文章将介绍风险。
时间无限,生命有限,强烈建议您赶紧使用计算机程序来帮您进行财务计算和推演,手算真的不足以支撑您的欲壑!
正文起:
对普通投资者来说,资产收益率体现了该资产的投资机会,并且与其投资规模无关;资产收益率序列比价格序列有更好的统计性质。为认知清楚收益率的本质,有必要先搞清下面几个概念。
一、单项资产收益率
1、单期简单收益率
如果从第t-1 天到第t天(一个周期)持有某项资产,则该项资产的简单收益率为:
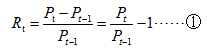
则:
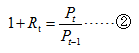
2、多期简单收益率
如果从第t-k天到第t天,在这k天持有某项资产(k个周期),则该项资产的k期简单收益率为:
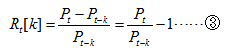
则:
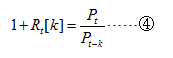
又:
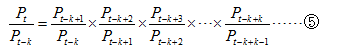
即:
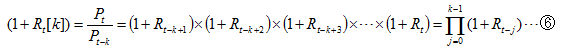
故:
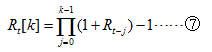
即:单项资产持有k期的简单收益率等于它所包含的k个简单收益率的乘积减去1。
3、持有K期的年化收益率为:
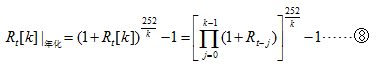
二、投资组合收益率
投资组合收益率是投资组合中各单项资产收益率的加权平均数。权重为投资金额的占比。
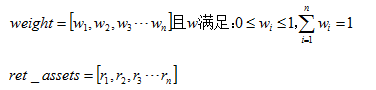
所以:

即:
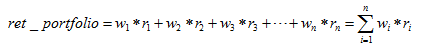
三、计算程序
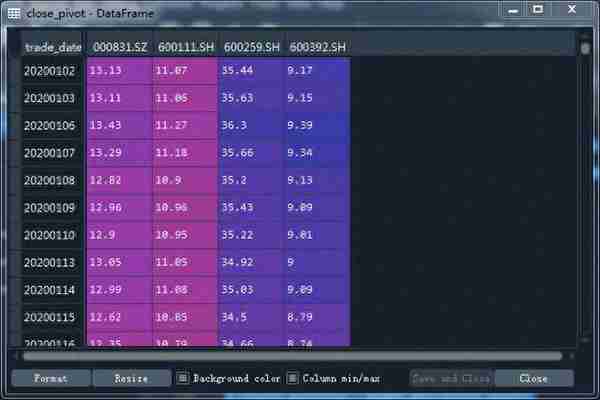
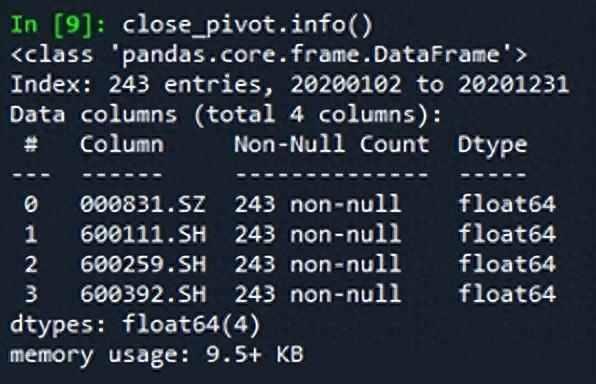
# -*- coding: utf-8 -*-"""Created on Thu Sep 29 17:08:53 2022@author: zgrweixin ID: """import warningsimport pandas as pdimport numpy as npimport tushare as tsimport matplotlib.pyplot as pltpro = ts.pro_api()# 股票投资组合:盛和资源,北方稀土,广晟有色,五矿稀土 tickers = '600392.SH, 600111.SH, 600259.SH, 000831.SZ' # 投资权重 weight = pd.DataFrame([{'000831.SZ':0.3,'600111.SH':0.3,'600259.SH':0.15,'600392.SH':0.25}]) # 1年的交易数据 data = pro.daily(ts_code=tickers , start_date='20200101', end_date='20201231')# 查看是否有空值:没有空值data.info()# 对收盘价进行透视close_pivot = data.pivot_table(values="close",index='trade_date',columns='ts_code')close_pivot.info()# 对返回值进行检查def _check_returns(returns):# Check NaNs excluding leading NaNsif np.any(np.isnan(returns.mask(returns.ffill().isnull(), 0))): warnings.warn("Some returns are NaN. Please check your price data.", UserWarning )if np.any(np.isinf(returns)): warnings.warn("Some returns are infinite. Please check your price data.", UserWarning )# 根据价格计算日收率def returns_from_prices(prices, log_returns=False):""" Calculate the returns given prices. :param prices: adjusted (daily) closing prices of the asset, each row is a date and each column is a ticker/id. :type prices: pd.DataFrame :param log_returns: whether to compute using log returns :type log_returns: bool, defaults to False :return: (daily) returns :rtype: pd.DataFrame """if log_returns: returns = np.log(1 + prices.pct_change()).dropna(how="all")else: returns = prices.pct_change().dropna(how="all")return returns# 根据价格计算各单项资产年收益率def mean_historical_return( prices, returns_data=False, compounding=True, frequency=252, log_returns=False):""" Calculate annualised mean (daily) historical return from input (daily) asset prices. Use ``compounding`` to toggle between the default geometric mean (CAGR) and the arithmetic mean. :param prices: adjusted closing prices of the asset, each row is a date and each column is a ticker/id. :type prices: pd.DataFrame :param returns_data: if true, the first argument is returns instead of prices. These **should not** be log returns. :type returns_data: bool, defaults to False. :param compounding: computes geometric mean returns if True, arithmetic otherwise, optional. :type compounding: bool, defaults to True :param frequency: number of time periods in a year, defaults to 252 (the number of trading days in a year) :type frequency: int, optional :param log_returns: whether to compute using log returns :type log_returns: bool, defaults to False :return: annualised mean (daily) return for each asset :rtype: pd.Series """if not isinstance(prices, pd.DataFrame): warnings.warn("prices are not in a dataframe", RuntimeWarning) prices = pd.DataFrame(prices)if returns_data: returns = priceselse: returns = returns_from_prices(prices, log_returns) _check_returns(returns)if compounding:return (1 + returns).prod() ** (frequency / returns.count()) - 1else:return returns.mean() * frequency# 返回单项资产日收益率(根据收盘价计算)returns_assets_daily = returns_from_prices(close_pivot, log_returns=False)# 日收益率曲线(日收益可视化)returns_assets_daily.plot(subplots=True,figsize=(8,6))# 日收益率直方图returns_assets_daily.hist(bins=20)# 日收益率极差、四分位差、方差、标准差和离散系数ret_des = returns_assets_daily.describe().Tret_des['var_coef'] = ret_des['std']/ret_des['mean']ret_des = ret_des.T# 计算投资组合的收益率def _objective_value(w, obj):""" Helper method to return either the value of the objective function or the objective function as a cvxpy object depending on whether w is a cvxpy variable or np array. :param w: weights :type w: np.ndarray OR cp.Variable :param obj: objective function expression :type obj: cp.Expression :return: value of the objective function OR objective function expression :rtype: float OR cp.Expression """if isinstance(w, np.ndarray):if np.isscalar(obj):return objelif np.isscalar(obj.value):return obj.valueelse:return obj.value.item()else:return objdef portfolio_return(w, expected_returns, negative=True):""" Calculate the (negative) mean return of a portfolio :param w: asset weights in the portfolio :type w: np.ndarray OR cp.Variable :param expected_returns: expected return of each asset :type expected_returns: np.ndarray :param negative: whether quantity should be made negative (so we can minimise) :type negative: boolean :return: negative mean return :rtype: float """ sign = 1 if negative else -1 mu = w @ expected_returnsreturn _objective_value(w, sign * mu)# 返回单项资产年收益率(根据收盘价计算)returns_assets = mean_historical_return(close_pivot)# 投资组合的年收益率returns_portfolio = portfolio_return(weight,returns_assets)returns_assets['portfolio'] = float(np.around(returns_portfolio.values, 6))# 收益率可视化returns_assets.plot(kind='bar',rot=45)plt.title('returns of assets and portfolio')plt.xlabel('tscode')plt.ylabel('annual returns')结果:
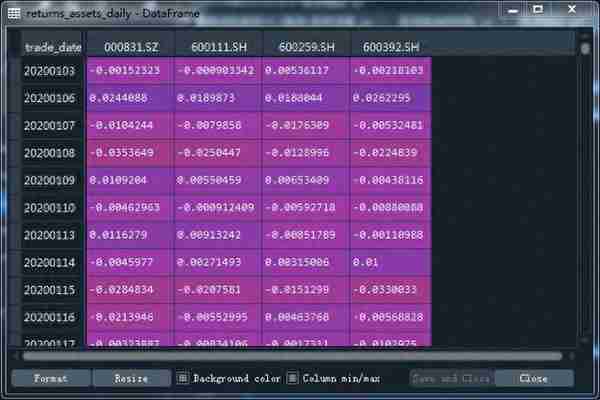
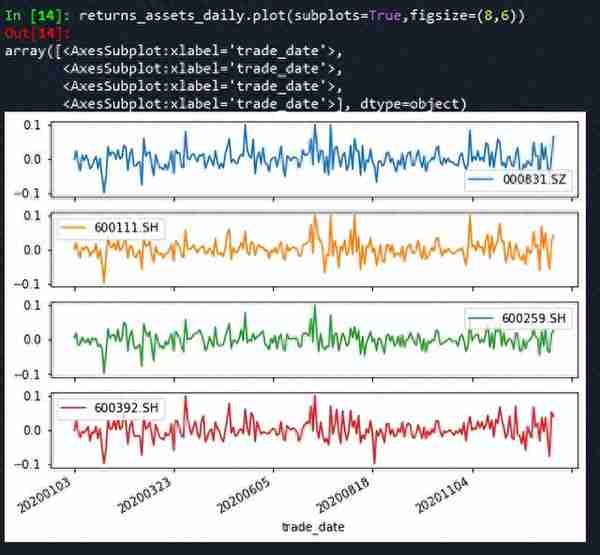
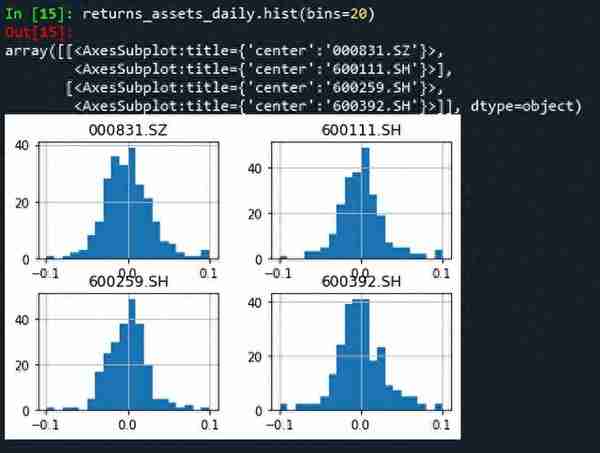
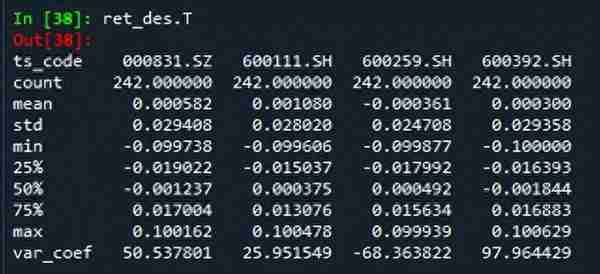
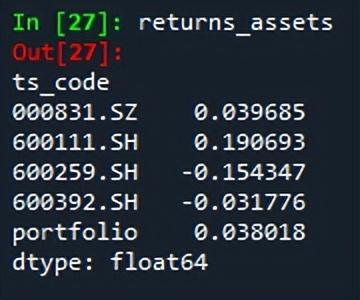
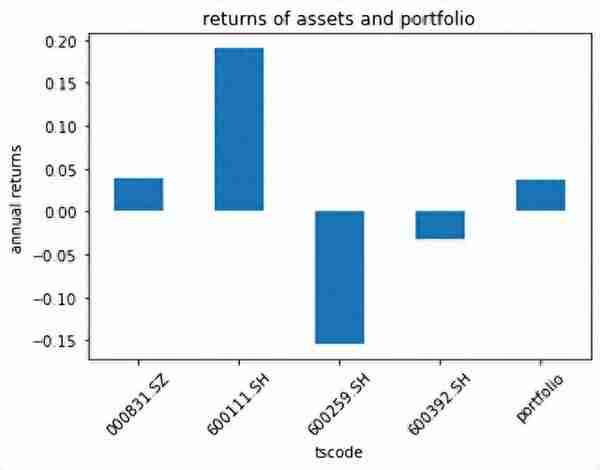
【仅供参考】
 BITGET交易所官网
BITGET交易所官网